Las coordenadas
Las coordenadas es la representación concreta de un punto en el espacio. En la vida diaria, se utilizan muy a menudo:
- para la representación de gráficos
- el juego de hundir la flota
- en el juego del ajedrez
- para introducir una dirección en el gps
- buscar el mapa de un tesorp
- para dibujar figuras simétricas
Para representar un punto en el espacio, es necesario imaginarse una recta horizontal ( eje x) y otra vertical vertical (eje y) que secruzan de forma perpendicular, es decir, formando un ángulo de 90 grados. Estos dos rectas forman un EJE CARTESIANO.
Cada uno de los ejes está dividido en partes iguales. El punto donde se cortan ambos ejes se llama punto origen (0,0)
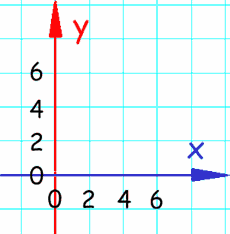
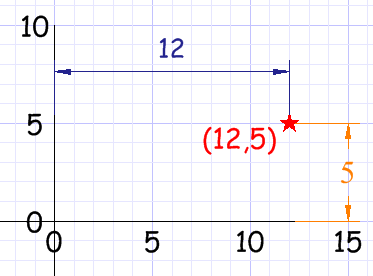
La representación de un punto viene dado por dos valores: Primero se escribe el valor del eje horizontal y luego el valor del eje vertical; separados por una coma. P(x,y) = P (5,12)
Practica las coordenadas en un plano de una calle pinchando aqui
Practica las coordenadas en un eje cartesiano pinchando aqui
Practica las coordenadas pinchando aqui
Practica las coordenadas pinchando en este otro enlace pulsando aquí
Simetrías
La simetría es la coincidencia de dos puntos o figuras en el espacio respecto a un eje, llamado EJE DE SIMETRÍA.

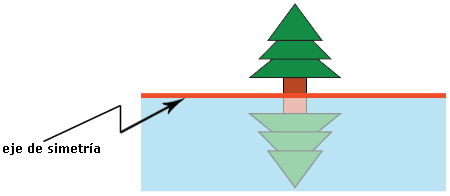




El eje de simetría es, pues, la línea imaginaria que resulta al dividir una figura en dos partes iguales.
Si todos los puntos de la figura están a la misma distancia respecto al eje de simetría, se llama SIMETRÍA AXIAL. Es la más común y es lo que conocemos como EFECTO ESPEJO.
Para dibujar figuras simétricas pincha aquí
Dibujar figuras simétricas anaya pincha aqui
Puntos simétricos pincha aquí
Parejas simétricas pincha aqui
Las traslaciones
En las traslaciones las figuras son iguales, es decir, tienen el mismo tamaño y la misma forma. Se trata de mover la figura completa en el espacio, de forma que todos los puntos nuevos están a la misma distancia del lugar que ocupaban inicialmente.

Dibujar figuras simétricas anaya pincha aqui
Puntos simétricos pincha aquí
Parejas simétricas pincha aqui
Las traslaciones
En las traslaciones las figuras son iguales, es decir, tienen el mismo tamaño y la misma forma. Se trata de mover la figura completa en el espacio, de forma que todos los puntos nuevos están a la misma distancia del lugar que ocupaban inicialmente.

Hacer traslaciones pinchando aquí
Las rotaciones o giros
Una rotación es girar algo tomando como referencia un punto.
Si el giro se realiza hacia la izquierda se dice que es un giro positivo (o giro antihorario). Si se realiza a la derecha se dice que es un giro negativo (giro horario).

Los giros se miden en ángulos. Pueden ir desde 0º (no se ha girado) a 360º (ha dado una vuelta completa).
Los giros más comunes son de 45º, 90º, 180º y 270º.
Las figuras son iguales pero están movidas según el ángulo que se haya girado.
Para ver la lección de forma más comprensiva, mira este video.
Practica la simetría y el giro aquí
Practica los giros dando orientaciones al robot
Practica los giros dando de comer al camaleón
Practica los giros dando de comer a la araña
Practica los giros con ángulos aquí
Practica los giros dando de comer al camaleón
Practica los giros dando de comer a la araña
Practica los giros con ángulos aquí
La escala
Los planos y mapas son representaciones de la realidad a tamaño reducido.
Las representaciones no se hacen ni a ojo ni al azar. Se sigue una norma llamada escala.
La escala es la relación que hay entre la representación en el plano y la realidad.
El resultado al dibujar a escala es una figura SEMEJANTE.
Practico el concepto de escala aquí
Aprende a utilizar la escala con este juego
Mide circuitos utilizando la escala
Resumiendo
Los mapas se dibujan a ESCALA y los puntos se dan dando unas COORDENADAS
Las coordenadas se representan dando el valor X y el valor Y de un eje cartesiano.
Las figuras pueden ser:
- SEMEJANTES: iguales en forma pero no en tamaño. Es decir, siguen una escala.
- IGUALES: iguales en forma y tamaño, pero trasladadas en el espacio
Existen tres tipos de movimientos en el plano:
- SIMETRÍA o efecto espejo
- TRASLACIÓN o movimiento de la figura en una dirección
- GIRO O ROTACIÓN o movimiento de la figura siguiendo un sentido horario o antihorario